Maths
But the angels said to them,
“Do not be afraid, I bring you good news that will cause great joy for all people.”
Luke 2:10
The angels brought the Good News that God’s son had been born. Jesus teaches us that we should value and love one another. By our example, our children are nurtured and encouraged to be kind and compassionate, showing God’s love to those around them and enabling everyone to flourish.
Everyone is included in the St Edburg’s family, inspired to make a positive change and encouraged to interact with the community around us.
All are valued, all are loved.
Maths Progression of skills
At St. Edburg’s C of E Primary School, we have adopted a mastery approach to the teaching of mathematics, which focuses on teaching for depth in understanding of mathematical concepts and ideas.
This approach enables all children to master the mathematics curriculum by building on their small steps. It draws heavily upon research conducted by the EEF (Education Endowment Fund) and their recommendations and is underpinned by the five ‘big ideas’ identified by the NCETM – Representation and Structure, Fluency, Variation, Coherence and Mathematical Thinking.
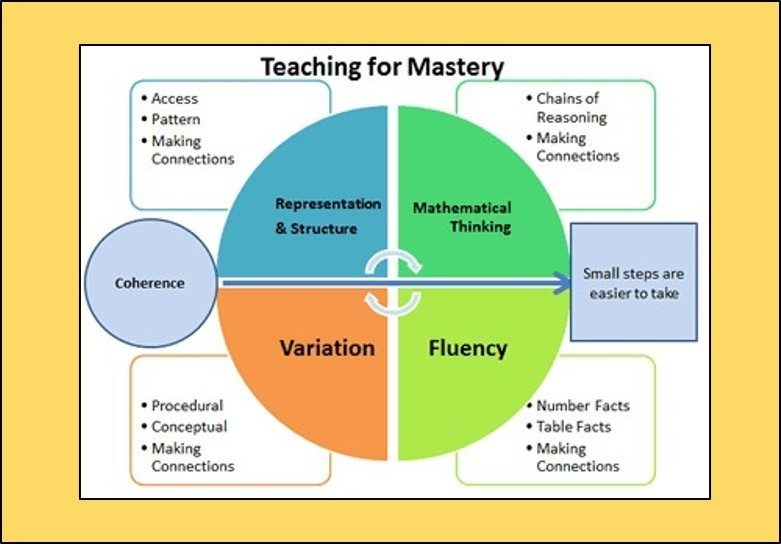
What is the intention of our curriculum?
Our aim is in line with the overall intent and key drivers of our whole school curriculum – to inspire, to include and to interact. We aim to develop and enable our children to become inquisitive and excited for maths and to know that it is an important creative process that helps us to understand and change the world. We want our children to experience the power and enjoyment of maths.
We further aim for our children to achieve a balance between what Richard Skemp identified as relational and instrumental learning, or which has more recently been referred to as conceptual and procedural understanding, through meeting the three fundamental aims of the National Curriculum for Mathematics:
- Fluency: become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately;
- Reasoning: reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
- Problem Solving: can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.
We view these aims as connected and interdependent aspects of our teaching, which will enable our children to make connections between mathematical concepts and apply their understanding in a range of contexts.
We want our children to:
- be efficient in choosing the most effective strategy/ies,
- see the benefit of working logically,
- become confident and independent mathematicians who can recall known facts, apply their knowledge to other areas of maths, other curriculum subjects and real life situations and
- communicate their reasoning and understanding in written form and orally.
Design
Whilst teaching the National Curriculum, our curriculum overview and planning are guided by the Curriculum Prioritisation documents published by the NCETM. Underpinning this planning are the NCETM Professional Development Materials and the Department for Education Mathematics Guidance which guide our pedagogical approach and enable teachers to plan engaging lessons that meet the needs of our children. Teachers are encouraged to use other materials such as White Rose and NRich to support their planning.
Through lessons designed to engage and excite the children, small steps for both conceptual and procedural understanding are planned for, giving consideration to common misconceptions that are likely to occur.
We recognise that it is important for teachers to be free to extend the time period over which a topic is taught in order to address gaps which are hindering the children’s ability to learn new content or should they feel that a depth of understanding has not been achieved. However, we expect all topics within the National Curriculum to have been covered to some degree over the year. Gaps will be identified in a timely manner by class teachers so that they can be addressed through same day intervention, or even by the next teacher.
Teachers will model and children will use concrete, pictorial and abstract models for each topic (appropriate to the learning context). Research conducted by the EEF underpins our expectation that both manipulatives and representations will be used in all year groups and across all ability groups to support learning before procedural methods are used; this will support our aim to help children become confident and independent mathematicians, allowing children to select from a range of strategies for both efficiency, to support success and deepen understanding.
Procedural methods for calculation are taught alongside mental methods for fluency and variation. Children will be expected to apply this learning within a range of contexts rather than completing extended procedural practice. Fluency does not always equate to speed but to efficient choice of strategy, which may well increase speed, particularly when trying to recall times tables.
To encourage the inquisitiveness and excitement within our children, we engage them in lots of discussion to help them work towards clear and concise explanations and reasoning. Teachers model the use of stem sentences for the children to use in their discussions and in their recording of work.













